PHOTOGRAPH BY NED MATURA
BY PALMER R. COOK, OD
At the end of the rainbow is a pot of gold, and over the rainbow is where bluebirds fly, or so they say. Pots of gold and bluebirds aside, rainbows are generally unwelcome visitors when it comes to your patients’ spectacle lenses and retinal images.
It is rare that a patient will actually mention the colored fringes or “rainbows” caused by chromatic aberration. Much more common comments are, “I can’t see with these,” or “These lenses are just not right.” It’s frustrating to you as an eyecare provider and disappointing to your patient when aberrations of any kind interfere with the performance of new eyewear.
The effects of chromatic aberration result from a combination of the Abbe value of the lens material, the prescription, the point at which the patient’s line-of-sight intersects the lens and the distance from the object being viewed.
DIOPTRIC SPREAD
IOphthalmic lens materials bend light by slowing it down. The amount of slowing (and bending) varies depending on the color (wavelength) of the light passing through the material. In the U.S. yellowgreen (the exact wavelength is 587.56 nm) is used throughout most of the ophthalmic industry for measuring lens power. This standardization keeps us all in step when considering the power of lenses. A lens that measures +5.00, for yellow-green light will measure slightly more than +5.00 for blue light and slightly less than +5.00 for red light. This difference in power can be called the “dioptric spread” between red and blue light for that particular combination of power and lens material.
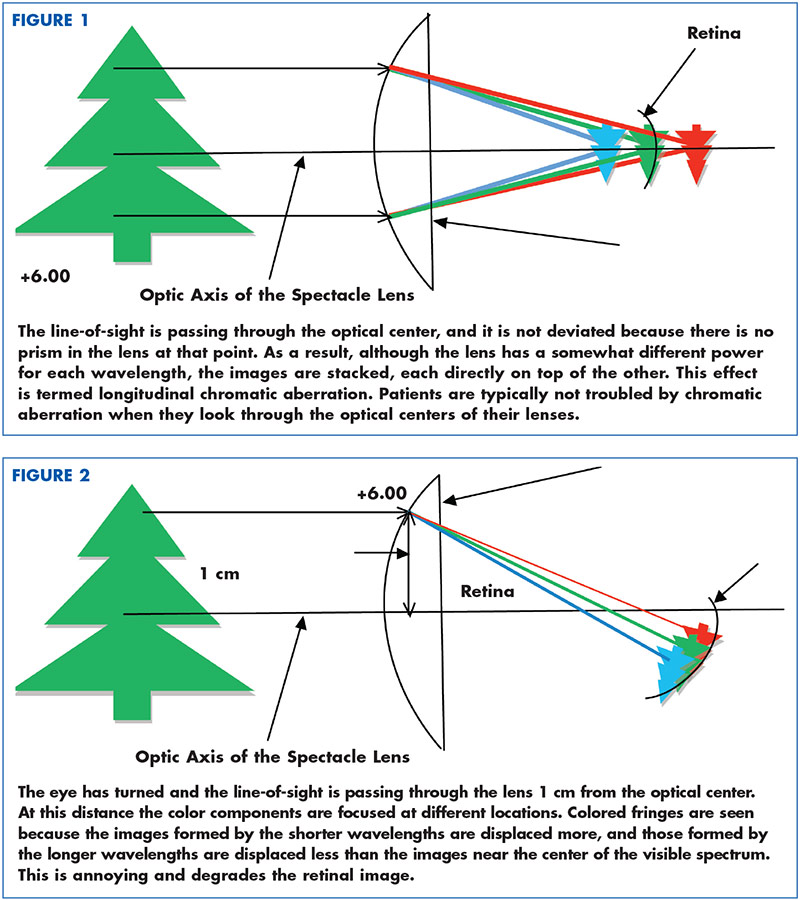
It is quite easy to determine the dioptric spread of any lens material. Simply divide the power of the lens by the Abbe value of the material. For example a +6.00 lens made of a lens material with an Abbe of 30 will have a dioptric spread of 6 ÷ 30 or 0.2 diopters. That means the lens will have a power of about +6.10D for blue light (486.13 nm), +6.00D for yellow-green light (587.56 nm) and +5.90D for red light (656.27 nm). Will this range of powers cause problems for your patient? Usually not—as long as your patient looks through the optical center of the lens! The reason is because the images formed by the various wavelengths of light passing through the lens are essentially stacked directly in front of and behind one another (Fig. 1).
PRENTICE’S LAW
Prentice’s Law is the basis for understanding how Abbe value affects the performance of your patient’s lenses. When the patient’s line-of-sight passes through the optical center, no prism is encountered. When the patient looks away from the optical center, these stacked images are displaced by differing amounts, sort of like spreading a deck of cards across a table (Fig. 2). The result is a rainbow of blur or color fringes at the edge of contours within the patient’s field of view. The width of this rainbow is related to the Abbe value and the prism powers for the various wavelengths as determined by Prentice’s Law. The color fringes are further apart from red to blue for a low Abbe lens and closer together for a high Abbe lens. It is important to recognize that a lens has not one power, but differing powers depending on the wavelength that is being considered.
WHEN DOES IT MATTER?
The color fringes are wider from red to blue for a low Abbe lens and narrower for a high Abbe lens. The range of powers for any lens is expressed in diopters. “Dioptric spread” can be used when referring to this range. The background of your lensometer is green to help you read the lens power in the yellowgreen range of the spectrum—around the helium d (He d) line of the spectrum, our U.S. standard.
For a +6.00 lens with a dioptric spread of 0.20 diopters (i.e., 6 ÷ 30), the power for red light is +5.90, and the power for blue light is +6.10. If the patient’s line-of-sight is 1 cm away from the optical center, the red component of your patient’s retinal image is displaced by 5.90Δ (1cm x 5.90 diopters), and the blue component is displaced by 6.10Δ (1 cm x 6.10 diopters). If the contour that is being viewed is vertical, and the base-apex line of the prism is horizontal (i.e., BO or BI), a red fringe will show on one side of the contour, and a blue fringe will appear on the other. The width of this spread of colors is 6.10Δ - 5.90Δ, or 0.20 prism diopters (0.2Δ). A lens made of a material with an Abbe of 30 and with a power of 10 diopters (either + or -) will have a dioptric spread of 10 ÷ 30 or 0.33 diopters. That means although the power of the lens using the U.S. standard of the He d line of the spectrum (587.56 nm) is +10 diopters; the power of the lens for blue light will be about +10.16 and for red light will be about +9.84 diopters. If you look through the optical center of the lens, the chromatic aberration has little effect on vision because the image formed by the red wavelengths, by the blue wavelengths and by all the wavelengths in the visible spectrum are stacked, one on top of the other. At most there may be a slight blurring because the slightly out-of-focus images at the far ends of the spectrum may be a bit larger than the in-focus part of this “longitudinally” stretched image. From a practical standpoint this blur is of little importance and color fringes are generally not visible—as long as the line-of-sight passes through the optical center and no prism is involved.
When the line-of-sight moves away from the optical center, prism is encountered. Prentice’s Law determines the amount of this prism. In the above example, when the line-of-sight moves to 1 cm away from the optical center, the He d line image will be displaced by 10 diopters x 1 cm or 10Δ. However the blue portion of the image will be displaced by about 10.16Δ and the image formed by the red portion of the image will be displaced by about 9.84Δ. The result is that the image is spread on the retina over a range of about 0.33Δ. It is this spread of images that is seen as the rainbow fringes characteristic of chromatic aberration.
The same 10 diopter lens made of a material with an Abbe of 42 will perform differently. Its power for the He d line is 10 diopters, but the power for blue light will be about 10.12 diopters and for red light will be about 9.88 diopters. The dioptric spread in this case is 10 ÷ 42 or about 0.24 diopters rather than the 0.33 dioptric spread with an Abbe of 30. The result is that the fringes are not spread over such a wide distance, and less “blur” is perceived, because a lens with a higher Abbe value was used.
TERMS
ABBE VALUE—A number (sometimes called the “V” value) that tells us how much chromatic aberration will result if the material is used as a lens. Lower Abbe values yield greater chromatic aberration, and higher Abbe values yield less chromatic aberration.
DIOPTRIC SPREAD—The difference in power from red light to blue light for any lens that is made of a material that slows light of differing wavelengths by differing amounts.
PRISM SPREAD—The displacement between red and blue images measured in prism diopters that arises when prism is encountered in a lens with chromatic aberration.
PRISM DIOPTER—The displacement of an image formed when the line-of-sight passes through a prism. If the angle of displacement is one prism diopter (1Δ), the image of an object at 1 meter will be displaced by 1 cm. The displacement is in the direction of the apex of the prism.
PRENTICE’S LAW—The power of the lens in diopters times the distance from the optical center to the point at which the line-of-sight passes through the lens equals the prismatic effect in prism diopters. The direction of the base of the prismatic effect is always toward the blue fringes.
OPTICAL CENTER—The point in the lens through which light passes undeviated.
THERE’S MORE TO THE STORY—DISTANCE
The location of the point at which the line-of-sight passes through the lens to the optical center of the lens and the power of the lens together determine the “prism spread” of the fringes. If this prism spread is 0.33Δ, then it represents a width of 0.33 cm if the object is 1 meter away. If the object is two meters away, the fringes are 0.66 cm wide. At 10 meters away they are 3.3 cm wide. It is apparent that the width of the fringes becomes greater as you look at objects at greater distances. This effect of distance can easily be seen by first looking at a target at a near distance through a plano prism made of a low Abbe material. Although some color fringes can be seen, the amount of blurring will be relatively minor. Then move away from the target to a longer distance and the width of the color fringes will be obviously greater, and the same will be true of the blurring caused by those fringes. See Fig. 3.

CLINICAL IMPLICATIONS
This distance factor should not be overlooked clinically. In one case a Montana rancher returned to his optometrist complaining that only if he looked “straight at something” could he see clearly. If he turned his head “just slightly” to the right or left, things got blurred. His distance Rx was in the 3.00D range, and his lenses were not defective. Switching him to a higher Abbe lens material gave him the vision he wanted.
In another case in the Midwest, a patient complained “things aren’t clear” with her new glasses (OD: -7.50 DS, OS: -8:50 -0.50 x 180, Add +1.00 OU, anti-reflective lenses were used). Her acuities were 20/15, OD, OS and OU. The Abbe of her lenses was 32, the index was 1.66. The prescribing doctor remade the lenses in a material with an Abbe of 42 and an index of 1.60. After a few days he reported, “She’s doing well with her glasses. She said she’s not straining as much for the distance. She seems happy with them.” In this case the vertical imbalance at near caused no problems. Significantly, the doctor mentioned that she didn’t comment about anything being unclear “in the office.” It’s obvious that we should not assume that a 20 foot “optical infinity” distance is a completely appropriate distance at which to evaluate a patient’s distance vision problems.
CHOICES
Manufacturers give density, Abbe and index. It’s up to you to use this information as you see fit. Standard plastic (density 1.35, Abbe 58 and 1.49 index), Spectralite (1.21 density, Abbe 47 and index 1.54) and Trivex (density 1.11, Abbe 42, 1.52 index and with high impact resistance) are among the many fine material choices that are available to you in various designs. By expressing your professional judgment about the choice of lens materials and other eyewear decisions in your post exam consultation, you can guide your patients to better performing eyewear.
SEE FOR YOURSELF
Order a plano, 6Δ, uncut prism lens in a low Abbe material from your preferred lab. Hold this lens so you can look through the optical center of your own spectacle lens (to eliminate any lateral chromatic aberration from your Rx) and examine several targets at various distances. This plano prism will induce the chromatic aberration that a patient with a 6 diopter Rx experiences 10 mm from the OC (about a 20-degree movement), or that a patient with 4 diopter Rx experiences looking 15 mm from the OC (about a 30-degree movement), or an 8 diopter Rx would give 7.5 mm from the optical center.
To really understand this aberration, it is important to experiment at a variety of distances. Moderately wide, black, vertical bars on a white background make a good target. The prism should be held with the base apex line at right angles to the bars (i.e., horizontally). To eliminate the chromatic aberration from the sides of the bars, rotate the lens by 90 degrees. This shifts the color fringes to the top and bottom of the bars. Any remaining blur along the sides of the bar is from some other source.
All ophthalmic lens materials have chromatic aberration, but problems related to it can be minimized. Patients most susceptible to the effects of this aberration include outdoor workers, pilots, patients who want better vision away from the centers of their lenses, those with prescribed prism and those who have mid-range and higher prescriptions. Until we have practical, chromatic aberration-free ophthalmic lenses we will not be at the end of the rainbow. If your patient returns saying he only sees those bluebirds, you might be close to the end of the rainbow, but it’s more likely another kind of healthcare professional should be called in.
RULES OF THUMB
1. Chromatic aberration, when the patient looks through the optical center of a lens, has relatively little effect on his or her vision.
2. The effect of chromatic aberration on vision is largely dependent on the amount of prism that the patient experiences when the lines-of-sight pass through the lenses at some point other than the optical centers.
3. The effect of chromatic aberration is also dependent on the Abbe value of the lens material. A lower Abbe value creates more chromatic aberration.
4. The effect of chromatic aberration is dependent on the viewing distance. Patients who are primarily at home or in their office can move their lines-of-sight further from the optical center of their lenses without experiencing so much difficulty with chromatic aberrations, and patients who spend more time looking at long distances tend to find the area of best vision restricted by chromatic aberration to a smaller area around the optical center of the lens.
5. Patients who wear single-vision readers will experience fewer problems related to chromatic aberration for reading as long as their lines-of-sight pass through, or tolerably near, to the optical centers of the lenses when reading. This argues for using high Abbe lenses and correct near PDs when recommending single-vision readers.
6. A patient who has a longer vertex distance will encounter more prism in swinging his lines-of-sight a given number of degrees from the optical center than a patient with a shorter vertex distance. This is a factor to keep in mind when selecting lens materials.
7. Because PALs typically have a prism neutralization point in the corridor area, patients may not have any area of their lenses that is prism-free for distance seeing. It is possible to write the prescription for PAL designs that will place the optical center in the distance area of the lens. Consult your lab about this. They should be able to produce the lenses as you want, but there will be a trade-off in lens weight and near vision performance.
Palmer R. Cook, OD, is an ophthalmic optics educator.