Vertically Challenged Part 1

By Andrew S. Bruce, LDO, ABOM

Unequal prescription powers, from eye to eye – it's the norm. When can it be a problem?

This two-part article reviews lens prescriptions and the potential issues prism might create when present, discusses eye associated conditions and recommends an evaluation process to determine an optimum solution.

It's helpful to start at the beginning when discussing prism . . .

Powered lenses are, in effect, prisms either mounted base to base (plus lenses), or apex to apex (minus lenses). The place where these imaginary prisms join is the lens' optical axis. A coincident light ray travels straight through, undeviated. That place is conveniently called the optical center (OC), though the optical center is actually a point that occurs along the optical axis. When light enters the lens at any point other than the OC, it is deviated. The degree of deviation is affected by:

• The power of the lens
• The distance of the point of entry from the optical axis (OC)
• The angle that the ray hits the lens surface
• Snell's Law
• The refractive index of the material
• The angle created when the ray exits the lens

When lenses are not centered for the eye i.e., the optical axis of the lens and the visual axis of the eye are misaligned, this results in an induced prismatic effect and a subsequent "shift" in the apparent placement of the object being viewed. This "shift" can potentially cause visual discomfort and patient adaptation issues to their new eyewear if it is not given its due attention.

Figure 1: OC location and the associated induced prism in lenses

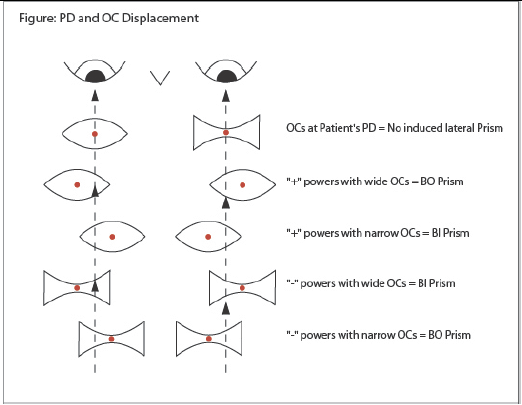
Horizontal displacement of the OC results in Base In (BI), or Base Out (BO) prism. As a result, this illustrates why accurate PDs are essential; otherwise the patient looks through lateral prism. The correct centering of lenses avoids unwanted prism. Similarly, vertical displacement of the OC induces Base Up (BU), or Base Down (BD) prism. Specification of OC height insures the patient is looking through the OC correctly.

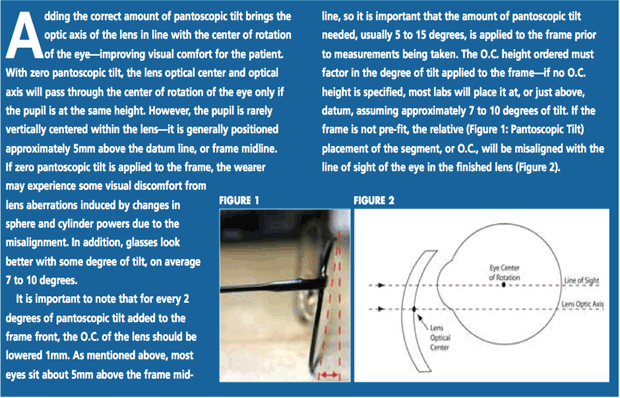
(Sidebar) OC location and lens tilt, shifting the optical axis.

PRENTICE RULE

A convenient way to calculate prism is Prentice Rule:

∆ = F x d
Prism (∆) = Lens Power (F) x Distance from the OC (cm) (d)

As the above equation shows, the amount of prism is directly proportional to lens power and the distance of the point of entry into the lens from the OC. Therefore, precise placement of the OC becomes increasingly more important as lens power increases.

Fig 2. Prism is affected by lens power and distance from the optical axis

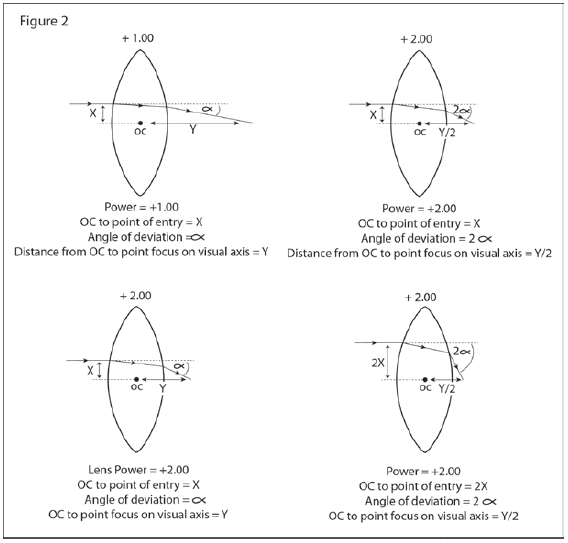
Although OC displacement in either meridian has the potential to cause visual discomfort, this discussion is primarily concerned with the effects of unequal vertical powers in a patient's right and left lens prescriptions and the associated problems they can potentially create if preventative measures aren't taken by the optician.

ANISOMETROPIA AND ANTIMETROPIA

According to "The Dictionary of Ophthalmic Optics" (Keeney, Hagman, & Fratello), Anisometropia is defined as, "Unequal refractive errors in the two eyes." It also defines Antimetropia as, "Opposite refractive errors in the two eyes – one plus, one minus."

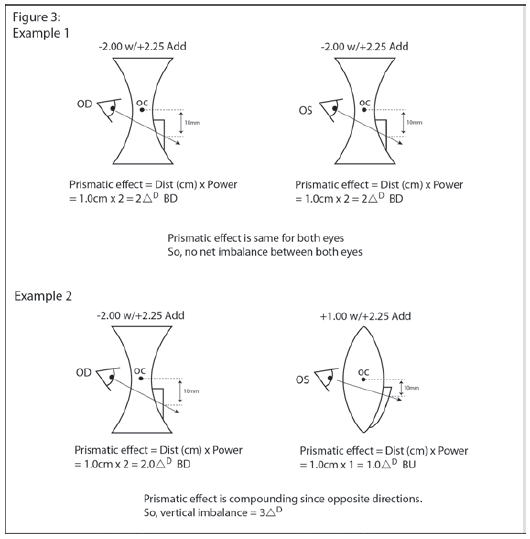
Either of these conditions can potentially induce significant differences in the prism created as the eyes move up and down when looking through lenses. The difference in the prism is called vertical imbalance. For example, patients viewing objects in their field of view with chin down, through the upper portions of the lenses, view the world through prism. If the lenses are of different powers (as most prescriptions are), then an imbalance in prism is created.

Any imbalance created can be reduced by raising their chin until there is minimal residual imbalance (less than 0.5 prism diopters). In single vision lenses, the patient can simply raise or lower their chin to look along the optical axis, where no deviation takes place. However, when dispensing a pair of multifocals, the patient is required to look through a location in the lens when reading, typically in the lower half, that is a significant distance away from the point of no prism – the distance OC. The patient is now effectively viewing the object through a prism and prismatic deviation occurs. As discussed earlier, this deviation is dependent on the lens power and the distance from the OC to the position in the lens through which the eyes are looking.

The direction of displacement is dependent on whether the lens is "plus" or "minus." When looking down from center, a "plus" lens induces a BU prismatic effect and the image appears to shift downwards; a "minus" lens induces a BD effect and the image appears to shift upwards. As an industry standard, a distance of 10mm below the distance OC is assumed for the point in the lens used for near work.

Calculating Vertical Displacement at the near point (NP)

Once again, using Prentice Rule:
Prismatic effect at NP = Lens Power vertically (90th meridian) x Distance from OC (cm)

Vertical imbalance affects stereopsis at the NP making near tasks difficult. Depending on the amount of imbalance, the patient can sometimes compensate for it. However, over time this can cause headaches and eye strain.

How much imbalance is too much?

The patients most often affected by vertical imbalance are multifocal wearers with good visual acuity in both eyes and an imbalance greater than 1.5D. When a patient only has good vision in one eye, this eye dominates and the brain suppresses the weaker eye. Therefore, any vertical imbalance present in the written prescription will not actually translate to becoming a vision problem for the patient.

NOTE: Correcting for induced vertical imbalance is especially critical when it is of recent onset. For example, following cataract, or refractive surgery on one eye only.

How do we fix this?

First, it is an effect of the prescription as determined by the doctor, so we cannot fix it, but we can correct for it. Some methods are capable of correcting for more imbalance than others.

Let's explore some options available and discuss the ordering process.

Single Vision Readers

As discussed previously, vertical imbalance is induced when the patient is looking through a point in the lens away from the OC, which happens when using a multi-focal lens. With a single vision lens, the patient has the option of looking directly through the OC by subconsciously re- positioning their head rather than needing to look down towards the lower part of the lens where the bifocal is typically located. Therefore, single vision readers are the simplest and probably most effective way to correct for vertical imbalance at the NP.

The Ordering Process

• Select a frame with a "B" measurement that allows for the frame to sit lower on the bridge enabling the patient to look over them for distance. This also helps direct the patient's line of vision through the optical center of the lens as their eyes naturally tilt down when performing near tasks.
• If using a larger frame, position the OC 5mm below the vertical geometric center of the lens. This, again, allows for the patient's natural tendency to drop their eyes when reading, and yet still be looking directly through the OC.
• Compute the single vision prescription for the working distance (WD) required – using either the full add, or a percentage of it as illustrated in Figure 4.

Figure 4: Add Power Calculation for Required Working Distance

Working Distance	Approximated % Add Power To Use
16" (40cm)	100% of Add
24" (60cm)	75% of Add
32" (80cm)	50% of Add
40" (100cm)	25% of Add

NOTE: In certain cases, the full add power may be written for a non-standard working distance (WD).  In this case, modifications will need to be made. However, this illustrates the process to follow. In addition, from this the add power required for a WD less than 16" can easily be calculated.  If filling an outside Rx and the add power is greater, or less than +2.50, a call to the prescribing doctor may be worthwhile to verify the WD for which it was written. For lower add powers, however, consider the patient's age and degree of presbyopia.  They may just be an early presbyope and require a lower add – a simple discussion with the patient can often clear up any confusion.

• Use the appropriate monocular PD: Apply an appropriate geometric conversion factor from figure 5 to the measured distance PD for the appropriate WD.

Figure 5: PD Conversion

Monocular  Distance PD	Approximate PD Conversion Factor for The Required Working Distance (WD)
	WD: 16"	WD: 24"	WD: 32"	WD: 40"
<31.5	-1.5	-1.0	-1.0	-0.5
>31.5	-2.0	-1.5	-1.0	-0.5

Example:

Monocular Distance PDs: OD: 33.0 OS:35.0            WD Requested: 32"            Full Add: +2.50

What Add Power is needed and what PD should be used?

Add Power for 32" = 50% of Add Power = +1.25            PD for 32": OD: 33-1 = 32 / OS: 35-1 = 34

Although a simple way to remedy the problem, it creates another – it is inconvenient! If the patient also needs distance correction, they have to constantly be switching between two different pairs of glasses. There has to be other ways! Do not despair, there are . . .

Dissimilar Segs

An alternative option, though rarely used today, is using dissimilar bifocal segs. This involves using the prismatic effect induced by the bifocal segment itself to offset the vertical imbalance induced by the distance lens when performing near tasks.

Let's explore this further...

A bifocal segment is effectively a miniature lens with an OC. Whenever viewing through a position in the lens away from the OC, prismatic effect is induced. When this miniature lens is combined with a distance lens – for example, a bifocal – this prismatic effect is separate from that induced by the distance lens. When both lenses incorporate the same style of bifocal, the same add power, and both are positioned at the same height, any prismatic effect induced by the bifocal will be the same for each lens, and thus neutralized. Since we are dealing with attempting to offset any induced prismatic effect by the distance lens, both bifocal segs will offset the same amount, and therefore have no net effect on correcting for imbalance between the two eyes.

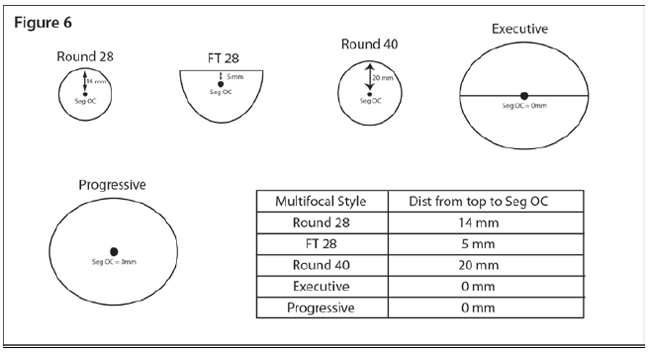
However, different bifocal styles have their OCs at different locations depending on their design.

Multifocal Styles and OCs

This knowledge can be used to offset small amounts of vertical imbalance.

(There are special considerations for both Executive style lenses as well as progressives since the SOLA E-Line lens is available as decentered with an OC 5mm below center and for many progressives, the center of the intermediate and near zone does not originate at the height of the distance OC as found in lined multifocals. These special considerations will be discussed in Part 2.)

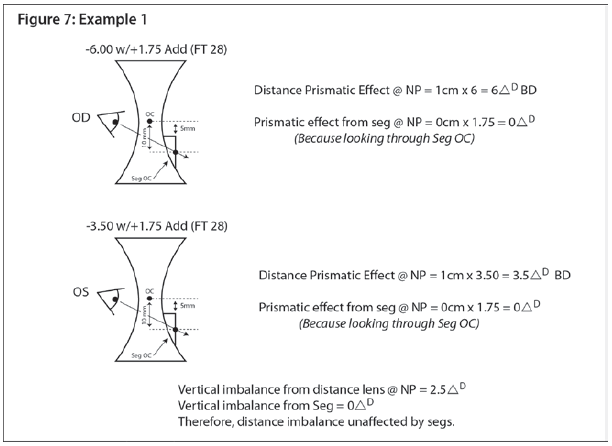
Example 1: Consider an anisometropic patient with the following Rx:

OD: -6.00             ADD: +1.75
OS: -3.50             ADD: +1.75

Such a prescription would result in 2.50D of vertical imbalance at the NP (Using Prentice Rule: See Figure 7, Example 1). A good assumption for the way that patients use bifocals is to look through a point 10mm below the distance OC for near which is 5mm below the top of the bifocal. If a FT 28 is used for each eye with its OC located 5mm below the segment top, the patient would be looking directly through the bifocal OC for near work, thus the vertical imbalance induced by the distance lens would remain unchanged.

However, if a different bifocal style is used for each eye, some of the imbalance can be reduced.

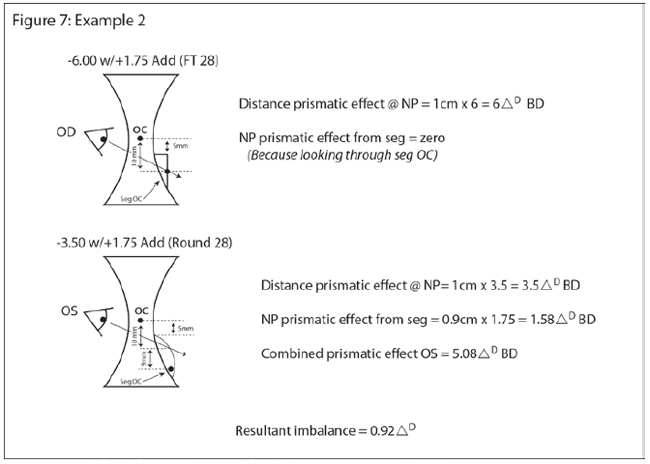
Example 2: A FT 28 with its OC 5mm below the segment top for the right eye and a round 28mm for the left whose OC is 14mm below. Both of these are positioned at the same height which is 5mm below the distance OC. When the patient looks down to read through the bifocal – a position 10mm below the distance OC (5mm below the top of both segs), the patient is looking through the OC of the FT28, so no prism is induced by it, and through a position 9mm above the round seg OC, so BD prism will be induced.

Assuming a +1.75 ADD power OU this would equate to:

OS Prismatic effect from seg at NP = Distance from OC x Power
=1.75 x 0.9cm = 1.58D BD

Combined prismatic effect OS = 3.5D BD from distance + 1.58D BD from seg = 5.08D BD

                        Prismatic effect at NP OD = 6.00D BD from distance only
                        Resultant Imbalance OU = 6BD – 5.08BD = 0.92D

This sounds more complex than it really is. Let's diagram it...

By always using the bifocal style with the highest OC on the lens with the most minus, or least plus power in the vertical meridian, this method can help offset some, if not all the vertical imbalance induced by the distance portion of the lens. In this example, using the combination of the FT28 on the right eye and the round 28mm on the left, the majority of the vertical imbalance is neutralized. Although there is still some residual imbalance, this solution may have resolved enough for it to no longer be problematic.

Example 3: By experimenting with other bifocal styles, for example, a round 40mm on the left eye by Younger - OC is 20mm away from the seg top which is fabricated 7mm below its distance OC, more imbalance can be neutralized.

Again, assuming a +1.75 ADD power OU this would equate to:

OS Prism effect from seg at NP = Distance from OC x Power
= 1.75 x **1.7cm = 2.98D BD.

NOTE: 1.7cm comes from = 17mm = the distance from the point in the bifocal used for near to its OC = 20mm – 3mm below seg top = 17mm = 1.7cm

Combined prismatic effect OS at NP = 3.50D BD + 2.98D BD = 6.48D BD
OD prismatic effect at NP = 6.00D BD (Same as prior example)
Resultant Imbalance at NP = 0.48D

So, using this round 40mm for the left lens would actually neutralize a little more vertical imbalance than necessary, but this demonstrates the concept and the residual 0.48 prism diopters of imbalance will most likely not be problematic. Cosmetically, this method is not as appealing as a method called Slab-Off (Part 2) and is somewhat restricted by the add power and size of the frame being used. However, for small amounts of imbalance where Slab-Off is not a viable option, or where affordability is an issue, this could be considered.

To Order Dissimilar Bifocals

1. Calculate the induced vertical imbalance the distance lens power and determine from evaluation of the patient's best-corrected acuities, if available, if the imbalance is going to create visual discomfort. If dealing with an Rx from another practice and best corrected acuities are not readily available, a call to the prescribing doctor might be in order.
2. Decide on the primary bifocal style going to be used and measure the fitting height.
3. Determine the distance of the segment top from the distance OC of this lens.
4. Factoring in a position of 10mm below the distance OC for near work, determine the prismatic effect induced by the primary segment itself at this position and calculate how much of the vertical imbalance induced by the distance lenses will be neutralized.
5. Calculate the residual imbalance.
6. Based on the Add Power, determine the most suitable bifocal style for the opposite lens that will neutralize the residual imbalance to an acceptable level as outlined in the previous paragraphs.
7. Place the bifocal style with the highest OC on the most minus, or least plus lens in the vertical meridian.

Part 2 will discuss the more contemporary methods used to correct vertical imbalance, slab off, and reverse slab for bifocals and progressives. It will also cover oblique power estimates and calculations and its relationship in determining vertical imbalance in sphero-cylinder lenses.