Sponsored by IOT
By Deborah Kotob, ABOM
Why compensate lenses? Free-form lens design and surfacing technology compensate the lens surface, making the effective power perceived by the patient in the primary gaze position match the prescribed power given by the refracting doctor. Why are they not the same? Short answer: The trial lenses used to refract the patient are flat and sit perpendicular to the patient’s visual axis in the primary gaze position, but when the lens is worn, it forms an oblique angle to the visual axis, inducing oblique aberration, changing the effective power perceived.

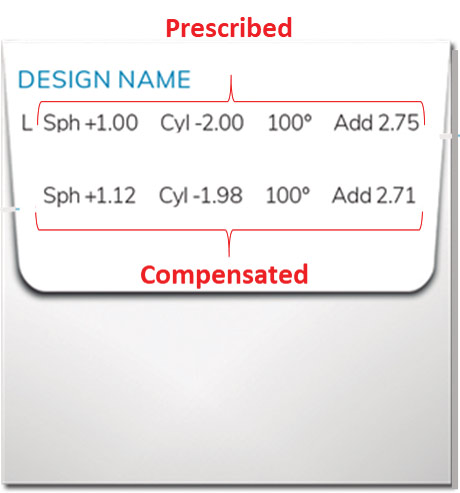
Why do verification power values differ from the prescribed power for compensated lenses? The power is not the power the patient perceives. The patient is looking through a lens tilted in front of their visual axis in the primary gaze position. If you were able to match this same tilt in the lensometer when verifying the power, you would see the power through the tilted lens equals the original prescribed power. Because the lens sits flat in the lensometer, the power readings reflect the effective power changes needed to compensate for the tilt angles in the as-worn eyewear.
OK, back to why compensate lenses? Ponder this: If the lens as worn in front of the visual axis matched all the trial lens parameters in the phoroptor, we would not need to compensate. The power perceived would match the power refracted. But the as-worn lenses don’t sit at a 90-degree angle to the visual axis; they aren’t always made of the same material index at the same base curve and sitting at the same vertex distance. Hence, effective power as worn differs from refracted power. Therefore, lens compensation.
Obliquity (no obliquity with flat perpendicular trial lenses—but there is obliquity with as-worn angled lenses) :
- Even before one considers eye rotation, oblique aberrations are preset in prescription lenses. Oblique aberrations are determined by prescription, base curve, tilt (panto and face-form), object distance and lens material refractive index. They occur with off-axis gaze where the visual axis rotates away from the lens’ optical axis or when the lens is tilted in front of the eye.
Oblique aberrations are optical power errors, with two components: error in the spherical component of the power, aka, mean power error and error in the astigmatic component of the power, known as oblique astigmatism.
- Oblique aberrations change the power: mean sphere (mean power error), astigmatism (oblique astigmatism).
Visualize how your patients wear their glasses. Do the bottom of the lenses sit in closer to the cheek forming a pantoscopic tilt angle in the vertical plane? Is there pantoscopic tilt angle around the horizontal axis? Tilting of a lens changes the resultant power: sphere power changes, cylinder is induced, with the axis oriented horizontally or vertically based on the axis of rotation. A lens tilted around the horizontal 180 degree axis has pantoscopic tilt, and a lens tilted around the vertical 90 degree axis has a wrap or panoramic angle (face-form).
You may wonder how compensated verification power values are calculated—short answer: with computational analysis by lens design software programs with highly sophisticated algorithms. Tina Lahti, vice president of sales and marketing for IOT, has this to say about trusting the math to the optical engineers and scientists: “IOT is an academic-based company. It is a spin-off of the University de Competence in Madrid. Our three founders were all professors at the University. Many of our researchers and optometrists graduated from there. Two of them head our research department and still teach there, Dr. Jose Alonso and Dr. Juan Quiroga, who co-authored Modern Ophthalmic Optics, the textbook, a cornerstone of learning in ophthalmic optics. Designing lenses and mathematical algorithms take years of higher education to earn an M.A. or Ph.D. in applied ophthalmic optics or a related field. My point is this: it’s not the kind of math that you or I work out on a whiteboard with a smelly marker, despite what you’ve seen on the Big Bang Theory. It is sophisticated complex math requiring advanced digital calculation technology. The real work happens with merit functions, not linear equations. If we don’t understand the effects of changing the fit parameters from the refracted parameters, compensated Rx verification numbers won’t make sense. Why is add power reduced by 0.08 diopters? Why the small amount of prism or change in power of the verification values? Hopefully, you now have a better understanding of these effects and know the reason for compensation and will confidently “trust the math.”